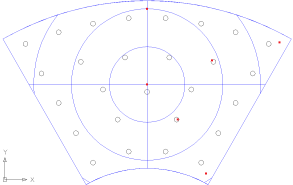
8, 8bに対して、固定支持点の位置を任意場所 から選択するのでなく、ホイッフルツリーの支持点27点の中から選択しての最小変形 を実現する3点の配置を調べてほしいということで再度計算。
27支持点の配置は、背面から最も距離が近い点で定義される鏡材中心点を通る半径方向
の線に対して対象であるが、8, 8bのように内側の固定点をその線上に載せようとしても
条件を満たす支持点は中央付近の1点しかないので、左右どちらかに移動させる必要がある。
FEM計算を簡単に行うため、鏡材に圧力をかける点は8と同じとする。
そのうえで、鏡材が線(面?)対象であることを利用し、固定点を線対称に配置することで
鏡像になる支持点配置に対してFEM計算を合計2セット行うことで、面全体に対しての
シミュレーションを実現することとした。
これらについて、内側の固定点が上から見て中心より左側にあるのを正、右側にあるのを
逆とし、逆側は ' 付きで表現している。
このため、以下のシミュレーション結果を見る際は2つの結果(12画像)をセットにして
解釈する必要があることに注意。
以下、最大へこみ変形量で議論しているが、厳密には圧力の作用点で判定する必要 がある。各パターンで最大へこみ変形量を示すモデルは最大へこみ変形量を示す場所と 圧力の作用点が近いので問題ないが、解釈においては注意すべき。 (つまりは、外周にないP1/P5/P6の3点に注意。)
27支持点の配置に対しての鏡材に圧力をかける点の配置は以下のようになる。
最大へこみ変形量の表は以下のようになる。単位はすべてμm/kgw
| Pattern | P1 | P2 | P3 | P4 | P5 | P6 | P1' | P2' | P3' | P4' | P5' | P6' | Max |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0.153 | 0.494 | 0.478 | 1.04 | 0.378 | 0.153 | 0.153 | 0.494 | 0.473 | 0.438 | 0.115 | 0.854 | 1.04 |
| B | 0.260 | 0.477 | 0.477 | 1.77 | 0.807 | 0.283 | 0.259 | 0.477 | 0.460 | 0.606 | 0.152 | 0.0869 | 1.77 |
| C | 0.239 | 0.789 | 0.399 | 1.24 | 0.441 | 0.316 | 1.24 | ||||||
| D | 0.449 | 1.268 | 0.058 | 1.000 | 0.299 | 0.409 | 0.449 | 1.269 | 0.057 | 0.456 | 0.123 | 0.422 | 1.269 |
| E | 0.243 | 0.760 | 0.535 | 0.461 | 0.110 | 0.884 | 0.243 | 0.760 | 0.053 | 0.957 | 0.320 | 0.274 | 0.957 |
| F | 0.235 | 0.780 | 0.053 | 0.423 | 0.094 | 0.285 | 0.235 | 0.780 | 0.546 | 1.080 | 0.375 | 0.137 | 1.080 |
| G | 0.260 | 0.848 | 0.539 | 0.426 | 0.106 | 0.095 | 0.260 | 0.849 | 0.345 | 0.827 | 0.193 | 0.340 | 0.849 |
| H | 0.116 | 0.510 | 0.456 | 0.391 | 0.115 | 0.085 | 0.116 | 0.509 | 0.752 | 0.937 | 0.260 | 0.269 | 0.937 |
最適配置はpattern gのものとなる。 ただし、力点配置を少しずらすともうちょっと大きくなる可能性はあり(後述)、 調査したほうがいいかもしれない。 が、これ以上小さくなるような配置はなさそうなので、調査したとしても最大値が ちょっと大きいものであるというのがわかる程度のはず。。
8bでの最適配置となった固定点配置に最も近い支持点を選択したもの。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 153nm/kgw |
 | 中央上を押した 変形は 494nm/kgw |
 | 右上を押した 変形は 478nm/kgw |
 | 右下を押した 変形は 1040nm/kgw |
 | 右中下を押した 変形は 378nm/kgw |
 | 右中上を押した 変形は 153nm/kgw | |
| 逆 |  | 中央を押した 変形は 153nm/kgw |
 | 中央上を押した 変形は 494nm/kgw |
 | 右上を押した 変形は 473nm/kgw |
 | 右下を押した 変形は 438nm/kgw |
 | 右中下を押した 変形は 115nm/kgw |
 | 右中上を押した 変形は 854nm/kgw |
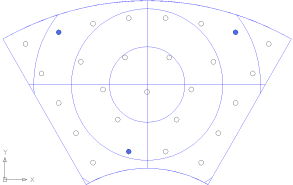
固定点が中心線よりずれたことで、少し最大変形量が1.04μmと大きくなっている。
aから内側の固定点を外にずらした。変形量は大きくなるはず。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 260nm/kgw |
 | 中央上を押した 変形は 477nm/kgw |
 | 右上を押した 変形は 477nm/kgw |
 | 右下を押した 変形は 1770nm/kgw |
 | 右中下を押した 変形は 807nm/kgw |
 | 右中上を押した 変形は 283nm/kgw | |
| 逆 |  | 中央を押した 変形は 259nm/kgw |
 | 中央上を押した 変形は 477nm/kgw |
 | 右上を押した 変形は 460nm/kgw |
 | 右下を押した 変形は 61nm/kgw |
 | 右中下を押した 変形は 152nm/kgw |
 | 右中上を押した 変形は 87nm/kgw |
内側の固定点と反対側の端の点がもっとも固定点は位置から離れているので、かなり大きくなった。
が、当然ながら外側のほうはあまり影響がない。
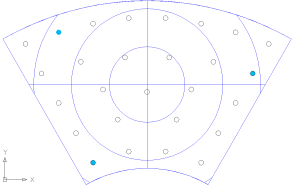
次は、内側の固定点から一番離れている固定点を少し下に動かしてみる。
bから内側の固定点から最も遠い固定点を下にずらした。変形がましになるかどうか。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 | 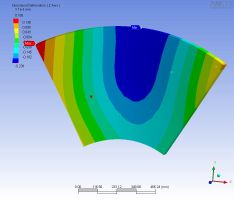 | 中央を押した 変形は 239nm/kgw |
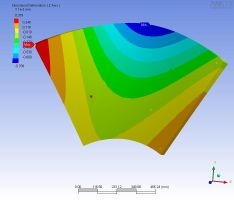 | 中央上を押した 変形は 789nm/kgw |
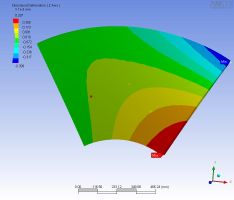 | 右上を押した 変形は 399nm/kgw |
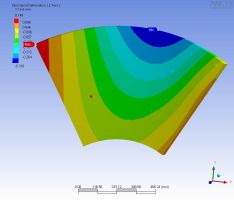
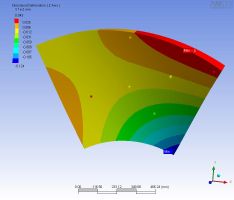 | 右下を押した 変形は 1240nm/kgw |
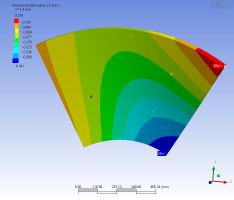 | 右中下を押した 変形は 441nm/kgw |
 | 右中上を押した 変形は 316nm/kgw |
前半をやったところで、最大変形量が1.2μmを超えたのでやめ。
内側の固定点は中心線に近いほうがいいということが判明。少なくとも最下列の場合は。
ひとつ上の列を試験するのはやってみてもいいかもしれない。
内側の固定点を中心線に近いほうに固定して、外側の固定点を移動させる。まずは両脇にずらす。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 449nm/kgw |
 | 中央上を押した 変形は 1268nm/kgw |
 | 右上を押した 変形は 58nm/kgw |
 | 右下を押した 変形は 1000nm/kgw |
 | 右中下を押した 変形は 299nm/kgw |
 | 右中上を押した 変形は 409nm/kgw | |
| 逆 |  | 中央を押した 変形は 449nm/kgw |
 | 中央上を押した 変形は 1269nm/kgw |
 | 右上を押した 変形は 57nm/kgw |
 | 右下を押した 変形は 456nm/kgw |
 | 右中下を押した 変形は 123nm/kgw |
 | 右中上を押した 変形は 422nm/kgw |
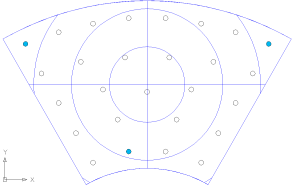
変形は外側の中央にある点でかなり大きくなった。これは前回の8,8bの解析結果とコンシステントである。
前回の解析ではある程度内側に寄せたほうが外側の円弧上で中央と両側のバランスがよくなるという結果
であったので、次はひとつを内側に寄せるのと、内側固定点と一番遠い固定点を下に移動させるのをやる。
外側の固定点の一つを内側へずらす。のパート１。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 243nm/kgw |
 | 中央上を押した 変形は 760nm/kgw |
 | 右上を押した 変形は 535nm/kgw |
 | 右下を押した 変形は 461nm/kgw |
 | 右中下を押した 変形は 110nm/kgw |
 | 右中上を押した 変形は 884nm/kgw | |
| 逆 |  | 中央を押した 変形は 243nm/kgw |
 | 中央上を押した 変形は 760nm/kgw |
 | 右上を押した 変形は 53nm/kgw |
 | 右下を押した 変形は 957nm/kgw |
 | 右中下を押した 変形は 320nm/kgw |
 | 右中上を押した 変形は 274nm/kgw |
少し最大値が小さくなっている。いい傾向？
これに対して、1点だけしかない側を下にずらしたものも試してみる。
外側の固定点の一つを内側へずらす。のパート２。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 235nm/kgw |
 | 中央上を押した 変形は 780nm/kgw |
 | 右上を押した 変形は 53nm/kgw |
 | 右下を押した 変形は 423nm/kgw |
 | 右中下を押した 変形は 94nm/kgw |
 | 右中上を押した 変形は 285nm/kgw | |
| 逆 |  | 中央を押した 変形は 235nm/kgw |
 | 中央上を押した 変形は 780nm/kgw |
 | 右上を押した 変形は 546nm/kgw |
 | 右下を押した 変形は 1080nm/kgw |
 | 右中下を押した 変形は 375nm/kgw |
 | 右中上を押した 変形は 137nm/kgw |
eより少し最大値が大きい。
左右で非均一な場合、ひとつしか点がない側をを外側に、二つあるのを内側に入れるほうがいい、という結果。
eの内側がよっているのと逆側の外側の点をひとつ内側にずらした。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 260nm/kgw |
 | 中央上を押した 変形は 848nm/kgw |
 | 右上を押した 変形は 539nm/kgw |
 | 右下を押した 変形は 426nm/kgw |
 | 右中下を押した 変形は 106nm/kgw |
 | 右中上を押した 変形は 95nm/kgw | |
| 逆 |  | 中央を押した 変形は 260nm/kgw |
 | 中央上を押した 変形は 849nm/kgw |
 | 右上を押した 変形は 345nm/kgw |
 | 右下を押した 変形は 827nm/kgw |
 | 右中下を押した 変形は 193nm/kgw |
 | 右中上を押した 変形は 340nm/kgw |
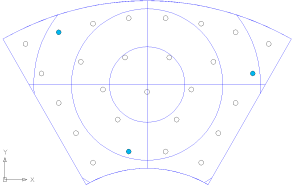
小さくなった。ただ、外側の力をかける点が中心ライン上(と固定点より外側)にしかないのが気にある。
固定点の中間点あたりではどうなる？
とりあえず、力点を増やすのではなく、動かした固定点をもうひとつ内側に移動させてみる。
今の最大点は外側中央の力点と内側固定点からと逆側の内周外側の点なので、
よりそれらに固定点が近くなるように。
gからひとつ内側にずらした。
| 変形 | 備考 | 変形 | 備考 | 変形 | 備考 | |
|---|---|---|---|---|---|---|
| 正 |  | 中央を押した 変形は 116nm/kgw |
 | 中央上を押した 変形は 510nm/kgw |
 | 右上を押した 変形は 456nm/kgw |
 | 右下を押した 変形は 391nm/kgw |
 | 右中下を押した 変形は 115nm/kgw |
 | 右中上を押した 変形は 85nm/kgw | |
| 逆 |  | 中央を押した 変形は 116nm/kgw |
 | 中央上を押した 変形は 509nm/kgw |
 | 右上を押した 変形は 752nm/kgw |
 | 右下を押した 変形は 937nm/kgw |
 | 右中下を押した 変形は 260nm/kgw |
 | 右中上を押した 変形は 269nm/kgw |
点4の内周の端が大きくなった。だめ。