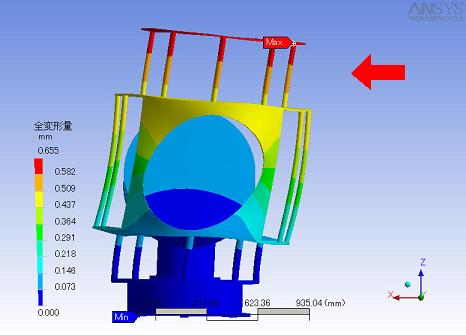
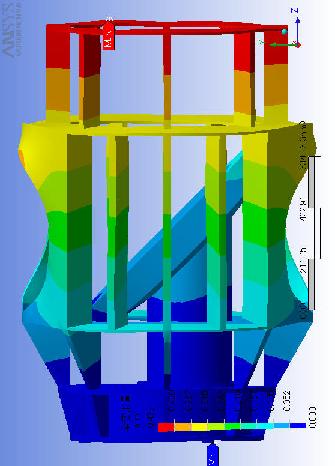
右上の図は鏡を正面から見た図です。力を矢印の方向にかけたので重力は矢印とは真反対の方向にかかっています。 アニメーションを以下におきました。
tertiaryunit_y.avi:+y方向から見た図(全変形量)
全体で一番歪みが生じたのはバッフル上部で0.655mm程地面側に下がりました。
また、バッフル中部につけた板もぐにゃぐにゃになっています。
 それぞれの構造に厳密な大きさはまだ確定していないので、板などの厚みや管の長さ、太さは適当な値を入れています。(右図参照)
それぞれの構造に厳密な大きさはまだ確定していないので、板などの厚みや管の長さ、太さは適当な値を入れています。(右図参照)
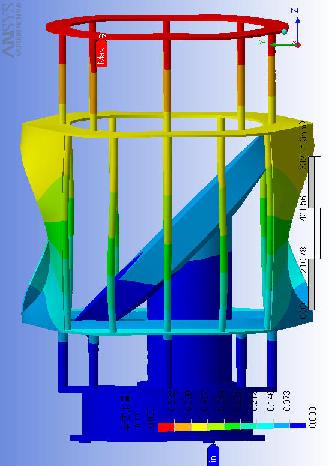 左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。

右上の図は鏡を正面から見た図です。力を矢印の方向にかけたので重力は矢印とは真反対の方向にかかっています。
アニメーションを以下におきました。
tertiaryunit_y.avi:+y方向から見た図(全変形量)
全体で一番歪みが生じたのはバッフル上部で0.655mm程地面側に下がりました。
また、バッフル中部につけた板もぐにゃぐにゃになっています。
| 全体[um] | x軸[um] | y軸[um] | z軸[um] | |
|---|---|---|---|---|
| 変形量(最大) | 655 | 0.3 | 105 | 139 |
| 変形量(最小) | 0 | -647 | -96 | -144 |
 90°に傾けたときの歪みは土台部分の変形が原因となっているので土台をしっかりさせるために放射状のリブを配置します。
90°に傾けたときの歪みは土台部分の変形が原因となっているので土台をしっかりさせるために放射状のリブを配置します。
 左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
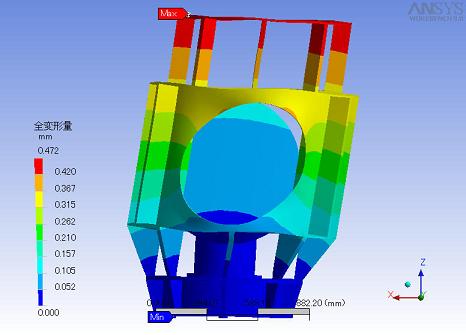
右上の図は鏡を正面から見た図です。向かって右に重力がかかっています。
アニメーションを以下におきました。
tertiaryunit2_y.avi:+y方向から見た図(全変形量)
全体で一番歪みが生じたのはバッフル上部で0.472mm程地面側に下がりました。
板にした方が若干ひずみが弱くなりました。
| 全体[um] | x軸[um] | y軸[um] | z軸[um] | |
|---|---|---|---|---|
| 変形量(最大) | 472 | 0.7 | 102 | 82 |
| 変形量(最小) | 0 | -470 | -76 | -82 |
特に、バッフルを除いた鏡と土台部分のみでの解析結果は以下のようになりました。
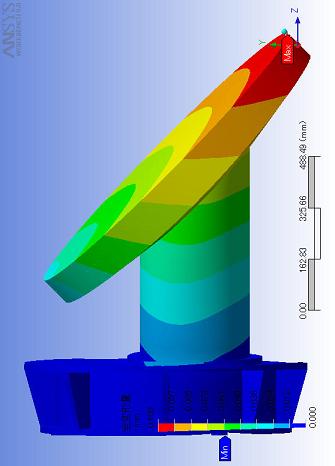 左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
アニメーションを以下におきました。
tdodaionly_x.avi:-x方向から見た図(全変形量)
(但しアニメーションは全体が横を向いています。)
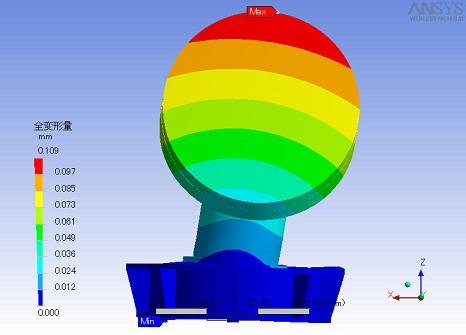
右上の図は鏡を正面から見た図です。向かって右に重力がかかっています。
アニメーションを以下におきました。
dodaionly_y.avi:+y方向から見た図(全変形量)
全体で一番歪みが生じたのは鏡部分で0.109mm程地面側に下がりました。
鏡本体の重みで土台が歪んでいるのが顕わに見えます。土台部分の強化が必要なようです。
| 全体[um] | x軸[um] | y軸[um] | z軸[um] | |
|---|---|---|---|---|
| 変形量(最大) | 109 | -109 | 2 | 39 |
| 変形量(最小) | 0 | 0.30 | -2 | -39 |
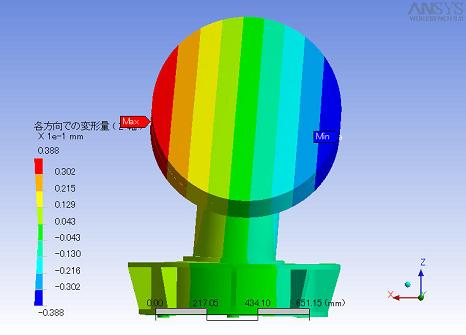
更にz軸方向の変形のみを表した図は右のようになっています。(紙面向かって手前が+y方向です。)
また、各部品の質量は、
 右図のように、鏡面の上四半点をA、左右四半点をそれぞれB、Cとします。変形前の鏡面の法線ベクトルはベクトルABとベクトルACの外積から、法線ベクトル=(0,1/√2,1/√2)となりました。(鉛直方向からinclination45°の方向。)
右図のように、鏡面の上四半点をA、左右四半点をそれぞれB、Cとします。変形前の鏡面の法線ベクトルはベクトルABとベクトルACの外積から、法線ベクトル=(0,1/√2,1/√2)となりました。(鉛直方向からinclination45°の方向。)| ベクトル | AB | AC | 外積 | ⊿B | ⊿C | 外積の変化量 |
|---|---|---|---|---|---|---|
| x成分 | 400 | -400 | 0 | 0.039 | 0.036 | -30.2 |
| y成分 | 388.91 | 399.91 | 311128 | -0.0010 | -0.0008 | 0.9 |
| z成分 | -388.91 | -388.91 | 311128 | 0.039 | -0.039 | 0.3 |
 鏡の重みで土台が変形し、それが全体の変形に繋がっているようなので土台の上下の板と円筒の厚みを増やしました。
鏡の重みで土台が変形し、それが全体の変形に繋がっているようなので土台の上下の板と円筒の厚みを増やしました。
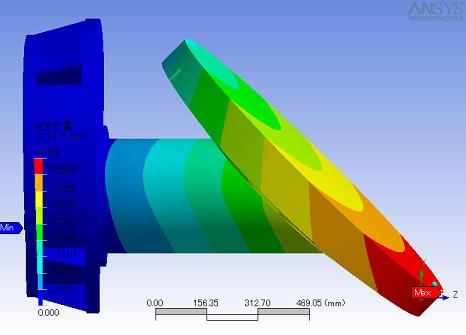 左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
左の図は鏡を横から見た図です。力を紙面に向かって奥にかけたので、重力は紙面から手前に向かってかかっています。
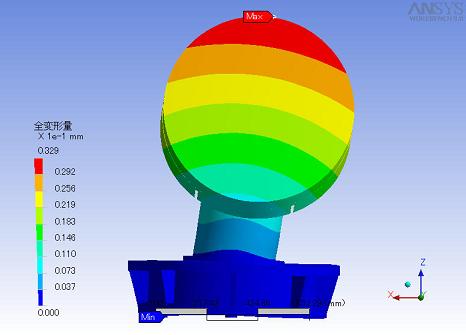
右上の図は鏡を正面から見た図です。向かって右に重力がかかっています。
アニメーションを以下におきました。
dodaionly2_y.avi:+y方向から見た図(全変形量)
全体で一番歪みが生じたのはバッフル上部で0.033mm程地面側に下がりました。
土台を強化したことと鏡+支持部分の軽量により歪みは1桁小さくなりました
| 全体[um] | x軸[um] | y軸[um] | z軸[um] | |
|---|---|---|---|---|
| 変形量(最大) | 33 | -33 | 0.7 | 12 |
| 変形量(最小) | 0 | 0 | -0.7 | -12 |
| ベクトル | AB | AC | 外積 | ⊿B | ⊿C | 外積の変化量 |
|---|---|---|---|---|---|---|
| x成分 | 400 | -400 | 0 | 0.011 | 0.011 | -8.98 |
| y成分 | 388.91 | 399.91 | 311128 | -0.00007 | -0.00002 | 0.06 |
| z成分 | -388.91 | -388.91 | 311128 | 0.011 | -0.012 | 0.06 |