- ● 反射・屈折
- 屈折の法則:n1 sinθ1 = n2 sinθ2
(n2 = -n1 とすると反射を表す)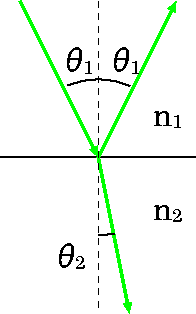
- ● レンズの仕組み
- 光軸:レンズ両面の曲率中心を結ぶ軸
焦点距離:平行光を入射させたときに集まるまでの距離
F比(口径比):焦点距離/レンズ口径で F/2.5 などと表す
F比が小さいとき「明るい」(fast)、大きいとき「暗い」(slow)という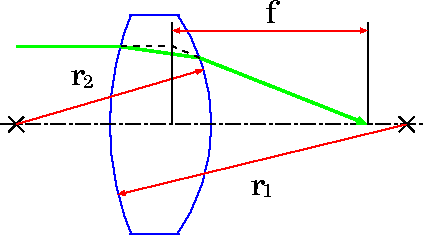
- ● 近軸公式
- 球面での屈折
- 曲率半径 r1 の球面(屈折率 n1,n2)
- 入射高 h1、傾角 u1
- sinθ~θ~tanθ、(cosθ~1) と近似
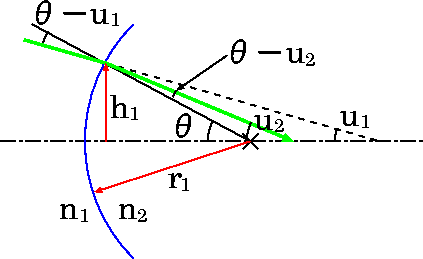
θ = h1/r1
n1(θ-u1) = n2(θ-u2)これより
n2u2 = n1u1+φ1h1 (1)
φ1 = (n2-n1)/r1φ1は光学面の power と呼ばれる値で、「集光力」を表す。
特に、空気中(真空中)の反射面では、φ1 = -2/r1 となる。
また、次の光学面までの距離を d とすると、h2 = h1-u2d (2)
n3u3 = n2u2+φ2h2このように順次 h,u を計算していくことができる。
特に d→0 の極限を「薄レンズ」といい、以下のように簡略化できる。n3u3 = n1u1+(φ1+φ2)h1
空気中(真空中)の薄レンズの場合、n3 = n1 = 1 なので
u3 = u1+φh1 (3)
φ = φ1+φ2と非常に簡単になる。
- ● 薄レンズの性質
- パワーφの薄レンズの焦点距離 f は(3)式より、
u2 = u1+φh1 = φh1
f = h1/u2 = 1/φ (4)(空気中(真空中)の反射面では、f = 1/φ = r/2 となる)
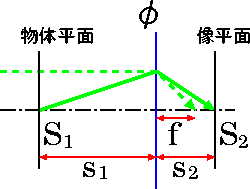
S1:物点 及び 物体平面
s1:物点距離
S2:像点 及び 像平面
s2:像点距離とすると、s1 = -h1/u1 (u1 は負), s2 = h1/u2 なので、
1/s2+1/s1 = 1/f (5)
の関係がある。
- ● 合成系の焦点距離
- 一般的な光学系における焦点距離は、以下の図のように定義されている。
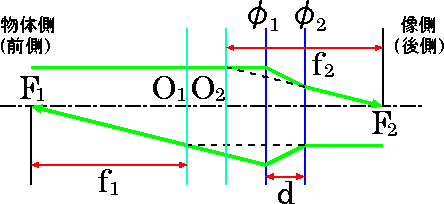
O1:物体側(前側)主点 及び 物体側(前側)主平面
F1:物体側(前側)焦点
f1:物体側(前側)焦点距離
O2:像側(後側)主点 及び 像側(後側)主平面
F2:像側(後側)焦点
f2:像側(後側)焦点距離間隔 d で並ぶ2枚の薄レンズ(パワー φ1, φ2)の場合には(2)(3)式より、
u2 = u1+φ1h1 = φ1h1
h2 = h1-u2d = (1-φ1d)h1
u3 = u2+φ2h2 = φ1h1+φ2(1-φ1d)h1 = (φ1+φ2-φ1φ2d)h1合成パワーは、
φ = φ1+φ2-φ1φ2d (6)
(密着して並べる場合は、各レンズのパワーの和が合成パワーになる)
また、空気中(真空中の)光学系の場合には、
f1 = f2 = 1/φ
となっている。
複数のレンズから成る合成系を簡略化して扱う場合には、単に主平面だけを描く。
上図の場合には、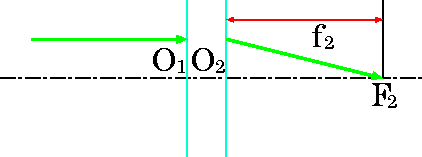
のようになる。
- ● 望遠鏡
- 入射瞳:光学系を通過する光束の太さを決める部分(望遠鏡の場合は対物レンズ口径)
射出瞳:(接眼レンズによる)入射瞳の像、目で見る部分はここ
主光線:入射瞳の中心を通過する光線
画角:入射光の傾角ω1
視野絞り:画角の最大値(視野)を決める窓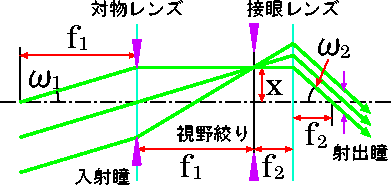
眼視望遠鏡の倍率は、
ω2/ω1 = f1/f2 = 入射瞳径/射出瞳径 (7)
で与えられる。
眼視で無く、CCD(または写真乾板)で観測する場合には、上図対物レンズ焦点部に直接置く。画角 ω1 で入射する光は、焦点面上でx = f1ω1 (8)
の位置に結像する。
- ● 収差
- 近軸計算では光学面は全て平面として扱われるが、実際の光学面は通常以下のような形を持つ。
z = cr2/(1+√(1-(1+k)c2r2)) (9)
書き換えると、
cr2+(1+k)cz2-2z = 0 (10)
c:曲率(curvature)、曲率半径の逆数
k:円錐定数(conic constant)
k>0 楕円面 k = 0 球面 -1<k<0 楕円面 k = -1 放物面 k<-1 双極面 屈折の法則、光学面形状とも正確な計算を行なった場合、焦点位置での近軸主光線からのずれの大きさは、光束半径(入射瞳位置での入射高) R と画角 ω に対し Rxtanyω の級数として展開する事ができる。光学面が(9)で与えられる様な偶関数である場合には、x+y が奇数の係数しか残らず、x+y = 3 の場合を3次収差、5の場合を5次収差などという。以下、x+y = 1,3 の場合に関して定性的に説明する。
x y 係数の意味 1 0 デフォーカス 0 1 常に0 3 0 球面収差 2 1 コマ収差 1 2 非点収差と像面弯曲 0 3 歪曲 デフォーカス:結像点からの光軸方向へのずれで、収差ではない。
球面収差:光束の外側の光と内側の光の結像位置のずれによる収差。近軸計算での像点位置では、像は広がったハロー状構造を持つが、最もシャープに結像する部分は少しずれて存在し、大きさを持った丸い像になっている。
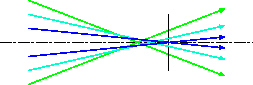
コマ収差:光束の外側の光の重心が像平面の半径方向にずれることによる収差。近軸計算での像点位置では、像は三角に広がった尾のような構造を持つ。
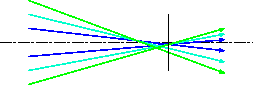
非点収差:像平面の半径方向とそれに直交する方向で、結像位置が異なることによる収差。近軸計算での像点位置では、像はデフォーカスのように丸く均一に広がった構造を持つが、前後にずれると縦や横に伸びた構造となる。
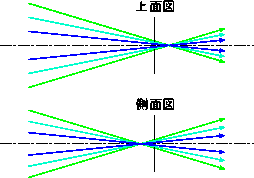
像面弯曲:像面の曲り。像面の半径方向とそれに直交する方向での弯曲の差が非点収差に相当する。光学系の中での凸面と凹面のバランスをとることにより減らすことができる。
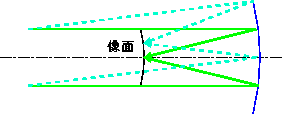
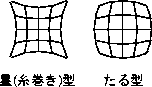
歪曲:像面の歪み。星(糸巻き)形とたる型がある。CCD を用いた現代の天文学では、ソフト的に除去することが可能である。
- ● 光路追跡計算
- (9)式などで与えられる光学面を組み合わせた光学系に対し、光路を正確に計算して計算するソフトウェアが幾つか市販されている。
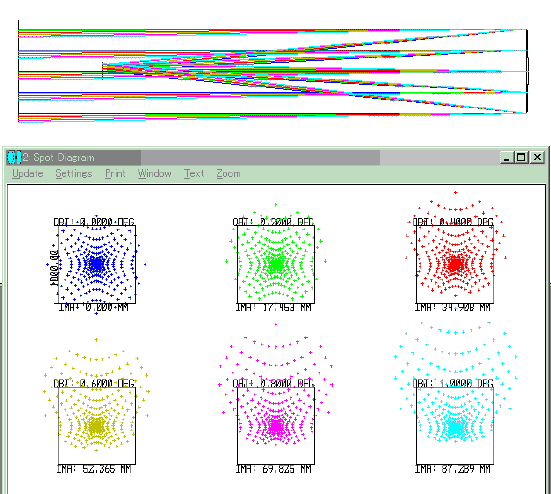
以下に口径 1m、焦点距離 5m (F/5.0) の反射鏡に対する簡単な計算例を示す。
曲率半径は焦点距離の2倍で 10m となっている。放物面鏡による集光。中心から 0.2°おきに 1°までの光束を計算。
画角に比例してコマ収差が増大していくのがわかる。
下図焦点部拡大図の四角は 1mm□。

球面鏡による集光。中心から 0.2°おきに 1°までの光束を計算。
球面収差は画角によらない事がわかる。
下図焦点部拡大図の四角は 1mm□。
- ● 回折
- 光は波の性質を持つため、限られた大きさの窓を通過する際には、回折により幾らかのエネルギーが異なる角度に向きを変えて進んでいく。この効果は、光学収差のように光学面の形状で決まるものではなく、通過する窓(または鏡)の大きさと外形のみで決まるものである。
以下のような幅 D の窓を平行光が開口に対し垂直に通過し、焦点距離 f の理想レンズで結像する状況を考える。
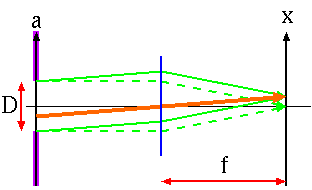
光は波の性質も持つため、軸上でない方向にも光は進行する。結像面上で x だけ軸からずれた所に集光する場合、開口上での進行方向のずれは x/f で、開口中心から a 離れた場所での光路差は ax/f となる。光の波長を λ とすると、位相差は2πax/λf となるので、これを開口幅全体で積分して重ね合わせる。
∫D/2-D/2 exp(2πiax/λf)da = (λf/πx)sin(πDx/λf)
光の強度は振幅の2乗なので、
焦点位置での明るさ ∝ (λf/πx)2 sin2(πDx/λf)= (D/X)2 sin2 (πX), X=Dx/λf
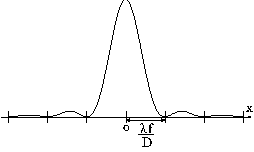
一般に、透過率 g(a,b) で与えられる開口窓に対し、光軸と平行に入射した平面波が、焦点距離 f を持つ無収差の理想光学系で集光される場合を考える。
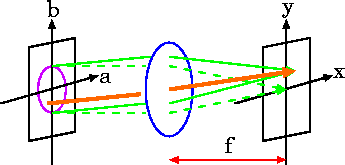
開口窓での回折効果により平面波の進行方向は変化するが、(8)式よりその傾角は焦点面上での像の座標(x,y)を用いて(x/f, y/f)となる(光学系の中心を通る光線を考えると分かりやすい)。開口窓上の座標(a,b)をこの傾角で通過する光線と、開口窓中心を通過するの光路差は ax/f+by/f と近似できるので、座標(x,y)に集光する光の復素振幅は光の波長をλとして、
U(x,y)∝∬g(a,b)exp[i(2π/λf)(ax+by)] da db (11)
と表される。これは x/λf = X, y/λf = Y としたときの2次元フーリエ変換の形となっている。即ち、g(a,b) に対し2次元フーリエ変換を行ない、(X,Y) = (x/λf, y/λf) とすれば U(x,y) を求めることができる。像の輝度分布は |U(x,y)|2 で求められる。
以下は、円形開口と矩形開口に対する計算結果である。

円形開口
矩形開口
回折像 (10%レベル)
回折像 (10%レベル)
回折像 (1%レベル)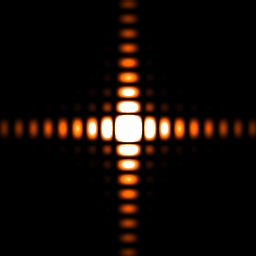
回折像 (1%レベル)特に、円形開口に対する回折光の強度分布はエアリーパターンと呼ばれる。
強度が初めに0になる半径(矩形開口の場合は強度が初めに0になる半幅)は、Δθ = 1.22λ/D [rad] (円形開口)
Δθ = λ/D [rad] (矩形開口) (12)で与えられ、理想光学系の分解能の限界を表す数値(回折限界)として用いられる。
望遠鏡の口径が大きく、波長が短い程、望遠鏡の分解能は高くなる。
(8)式のω1に上記Δθを代入することで、実際の像サイズを計算することができる。
- ● 屈折望遠鏡と反射望遠鏡
- 屈折望遠鏡
- 対物レンズを用いた望遠鏡で、光束内を遮るものがないためきれいな星像が得られるが、大口径化が難しいことと、波長による焦点距離の変化(色収差)がある。接眼レンズに凹レンズを用いるガリレオ式と、接眼レンズに凸レンズを用いるニュートン式がある。
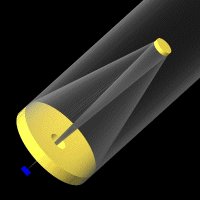
- 反射望遠鏡
- 対物レンズの部分に反射鏡(対物鏡)を用いた望遠鏡で、通常は焦点を光束外に出すための鏡(副鏡)が必要である。副鏡を支える構造物が光束を遮るため星像が劣化するが、大口径化が可能で、屈折望遠鏡に見られるような色収差がない。
- ● 直焦点(主焦点)
- 単一の鏡の焦点面を直接用いるもの。
利点:焦点距離を短くできるため広い視野の観測に適している
欠点:観測装置で光束が乱される
大型装置を付けるには望遠鏡全体の強度を増す必要がある
収差が大きいのでレンズなどの補正光学系が必要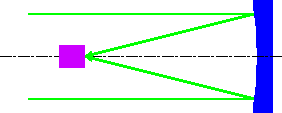
- ● ニュートン式
- 平面鏡で反射して直焦点を光束の外に出したもの。
利点:調整が簡単で、安価の眼視望遠鏡向き
欠点:主鏡のF値が小さい場合には副鏡が大きくなり不向き
大型装置を付けるには望遠鏡全体の強度を増す必要がある
収差が大きいのでレンズなどの補正光学系が必要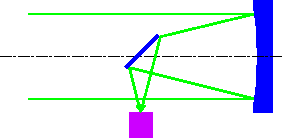
- ● マーチン式
- 穴空き平面鏡で反射して主鏡に光をあてる方式。
利点:焦点距離を短くできるため広い視野の観測に適している
スパイダーが不要できれいな像が得られる
欠点:大きな平面鏡が必要
収差が大きいのでレンズなどの補正光学系が必要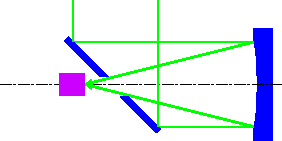
- ● カセグレン式
- 放物面の主鏡と凸双曲面の副鏡で主鏡の裏に光を集めるもの。
利点:望遠鏡の全長を短くできるため中~大口径望遠鏡に適している
欠点:(周りの空からの光を遮る筒状のバッフルが必要)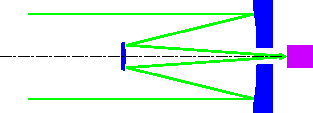
- ● グレゴリー式
- 放物面の主鏡と楕円面の副鏡で主鏡の裏に光を集めるもの。
利点:副鏡が凹面なので少し安価
直焦点に点光源を置くことにより、疑似星を作れる
欠点:望遠鏡の全長が長くなる
カセグレン式より副鏡から焦点までの距離が長くなる
(カセグレン式同様バッフルが必要だが、直焦点付近に穴あき板を置くだけでOK)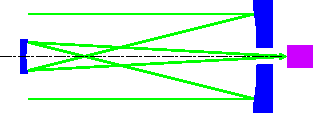
- ● ナスミス式
- カセグレン式に平面鏡を加え、望遠鏡の高度軸方向に導く方式。
利点:焦点部の高さが変わらないので、大型の観測装置を取りつける事が可能
欠点:カセグレン式より副鏡から焦点までの距離が長くなる
斜鏡を用いるため偏光が起こる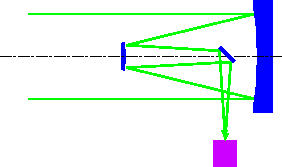
- ● クーデ式
- 数枚のリレー鏡で、別室に固定された観測装置に焦点を導く方式。
現在ではナスミス式の方が主流。
利点:大型の観測装置を取りつける事が可能
欠点:通常はリレー鏡の数が多く、光のロスが大きい
非常に狭い視野であることが普通
斜鏡を用いるため偏光が起こる - ● シュミットカメラ
- 球面鏡の主鏡の曲率中心に4次曲面の補正板を入れて、全画角に対する球面収差を補正した望遠鏡。球面鏡よりも補正板の方が高価であるため、補正板が入射瞳となる。
利点:超広視野
欠点:像面がかなり弯曲する
巨大な補正板が必要
観測装置で光束が乱される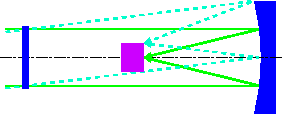
- ● リッチー・クレチェン
- カセグレン式の主鏡を放物面に近い双曲面に変え、球面収差とコマ収差を除いたもの(厳密には双曲面でもない)。
利点:カセグレン式より広視野
欠点:像面がやや弯曲するグレゴリー式でも同様な補正項を入れて広視野化する事が可能である。
- ● 3枚鏡望遠鏡
- 凹凸凹と3回反射して集光する望遠鏡。3回反射させることで非点収差や像面弯曲まで除くことができ、補正レンズも加えることで更に高次の収差の除去も可能である。鏡の配置位置の違いにより数種類の光学系が発表されている。
利点:超広視野
欠点:光学系が複雑で製造が難しい
観測装置で光束が乱される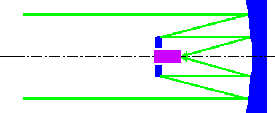
- ● 望遠鏡の架台
- 赤道儀式
- 北極星の方向(極軸)とそれに直交する方向(赤緯軸)の回転軸を持つ架台。極軸の等速回転により天体を追尾する。1980年代まで様々なタイプのものが作られたが、現在は大形のものは作られていない。以下は岡山天体物理観測所の 188cm 望遠鏡の例(イギリス型)。
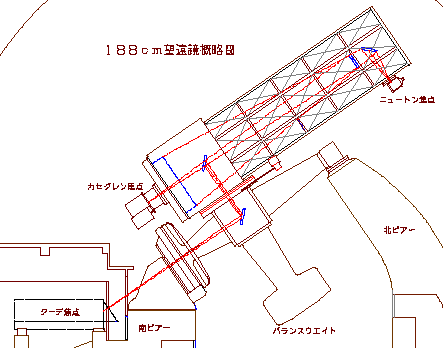
http://www.oao.nao.ac.jp/ - 経緯台式
- 垂直方向(方位軸)と水平方向(高度軸)の回転軸を持つ架台。両方の軸が速度を変えながら同時に回転することにより天体を追尾する。巨大望遠鏡に適した構造を持つのに加え、安定したナスミス台を持つため、1974年の BTA 6m 望遠鏡(旧ソ連・ゼレンチュクスカヤ)以降、徐々に経緯台式が主流となってきた。以下はすばる 8.2m 望遠鏡の例。
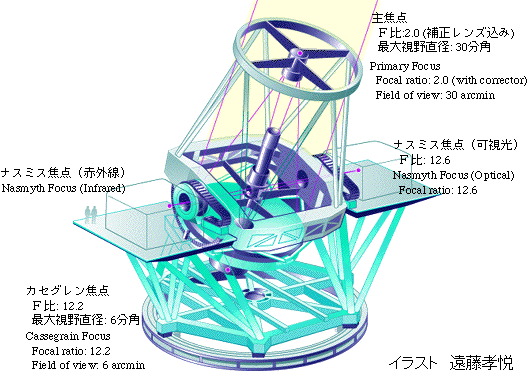
- ● 望遠鏡の口径
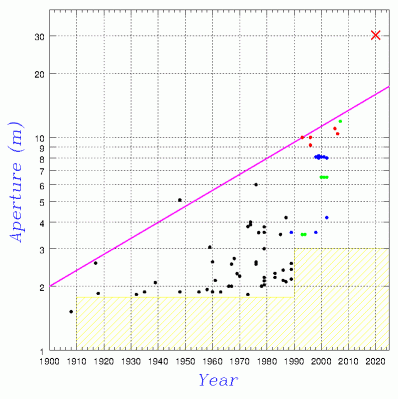
- 近代の巨大望遠鏡の建設は、Ritchey の Mt.Wilson 60,100インチ望遠鏡から始まり、40年で2倍ずつ口径が大きくなっている。2020年代には、口径30~40m の望遠鏡を建設する計画が現在幾つかの天文台で進められている。
点の色分けは以下の通り(詳細は「超巨大望遠鏡への道」参照)
● 通常の鏡:ガラスの固まりで厚さは直径の 1/8 程度。
● 分割鏡:鏡面を高精度位置制御で揃える技術が必要。
● ハニカム鏡:中空鏡で軽量強固だが、鏡内部の換気が必要。
● メニスカス鏡:薄い鏡で背面からの力制御で鏡面形状を制御。


https://www.mtwilson.edu/ https://sites.astro.caltech.edu/palomar/homepage.html
左より Ritchey の 60,100 インチ望遠鏡(フォーク型, ヨーク型)、Hale 200 インチ望遠鏡(ホースシュー型)
左2つは青板ガラス、Hale 望遠鏡はパイレックスガラスの主鏡を持つ。

https://www.keckobservatory.org/
Keck 10m 望遠鏡
18枚の分割鏡による初の分割鏡望遠鏡。 - ● その他の望遠鏡

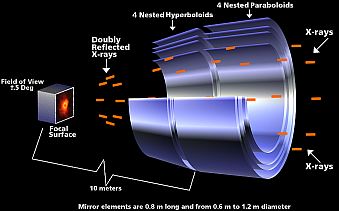
https://chandra.harvard.edu/
Chandra X線望遠鏡
X線は透過力が強いので、非常に浅い角度でないと反射することができない。

https://greenbankobservatory.org/ https://www.almaobservatory.org
Green Bank 100m 望遠鏡 / ALMA 電波干渉計
電波は光を波として記録できるので、個々の望遠鏡で取得された情報を計算機により干渉させることが可能である。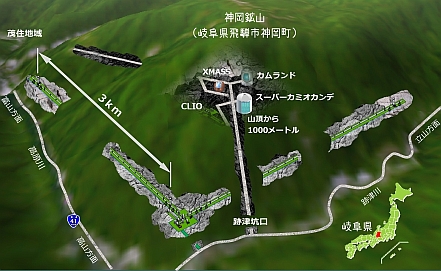
https://gwcenter.icrr.u-tokyo.ac.jp/
重力波望遠鏡
重力波は4重極波として伝わるため、直交する2方向の光路差を測定することで検出する。
3km に対し、1/1000Åの光路差の変化を測定を目指している。