Volume Binary Grating の効率計算
http://www.kusastro.kyoto-u.ac.jp/~iwamuro/HDS/rcwa.html

岩室 史英 (京大宇物)

●経緯

    CaHK 線用の UV 分光器の回折格子を VB(Volume Binary) Grating で製作する事を検討しており、理論的な効率予測が必要となったため、RCWA 法という手法を用いて効率を計算してみた。

●Volume Binary Grating とは

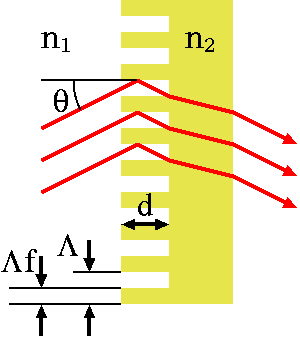
    Plymouth Grating Laboratory という会社が製作している櫛の歯状の回折格子で、VPH Grating のような使い方をするもの。エッチングで光学素材を直接加工して製作するようだ(上記リンクのページ参照)。

●RCWA (Rigorous Coupled-Wave Analysis) 法

    電磁波の境界問題を、接続層内部での状態を表す方程式を行列化して固有値分解し、それに対応する固有ベクトルで表されるモードで展開して入射側と射出側の境界条件で接続する、という雰囲気。こちらに非常にわかりやすい丁寧な解説があったので、この文書に従ってプログラムを作ってみた。

  • rcwa.c : プログラムのソース、./rcwa rcwa.dat で計算できる。
  • rcwa.dat : １行目が入力パラメータ(媒質１屈折率(n1), 媒質２屈折率(n2), λfrom, λto, Δλ, Groove密度(1000/Λ), Groove深さ(d), 幅比(f), 入射角(θ))で、２行目以降は計算の度に更新される(計算開始時は１行目の情報だけが必要)。
  • SiO2.tbl : 媒質の屈折率を数値ではなくファイルで渡すと、波長ごとに屈折率を変えて計算する。波長で昇順である必要がある。先頭の波長が３桁であれば単位は nm、４桁であればÅ、それ以外は μm であるものと判断される。

    計算の概要：
    上図の画面に対して垂直な方向の電磁波の成分が回折格子層内でのモード分けに用いられるので、垂直成分が電場である場合(TE 波、s 偏光)は電場で方程式を作り、垂直成分が磁場である場合(TM 波、p 偏光)は磁場で方程式を作る。式の形はどちらもほぼ同じになるが、TE 波の場合は固有値展開する行列が対称行列になるのに対し、TM 波の場合は非対称な行列になるため、固有値展開する場合に最も簡単な Jacobi 法を使うことができない。そのため、QR 法で固有値のみ先に求め、それを元にシフト付き逆反復法で対応する固有ベクトルを順に求める。

    固有値と固有ベクトルを求めたら、上述の解説文に従って接続層内部での進行方向と逆方向の状態に対応する c+,c- ベクトルを解くが、ここの計算は全て複素数で行う必要があるため、j を虚数単位として

    (Ar+Aij)(xr+xij)=yr+yij

    Arxr-Aixi=yr
    Aixr+Arxi=yi なので、

    (Ar -Ai)(xr)=(yr)
    Ai　Arxiyi

    のようにして実数の行列として解く。普通の正則行列なので逆行列は掃き出し法で計算できる。

●計算結果

    上記 Plymouth のページ 左下にある写真の格子のパラメータ(記号は上図参照)

    n1=1.
    n2=SiO2.tbl (合成石英を仮定, 1.471 固定値でも結果はあまり変化しない)
    λfrom=0.2 μm
    λto=0.6 μm
    Δλ=0.001 μm
    1000/Λ=2400 l/mm
    d=0.65 μm
    f=0.5
    θ=28.3°

    で±５次まで計算し、±２次を表示したものが以下左図。

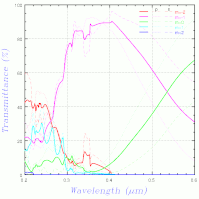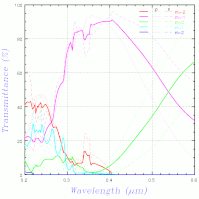
    上右図は、海老塚さんのお知り合いの方(岡本隆之さん、この本の著者の方)に計算して頂いた結果だが、ブリンクさせて比較すると少し異なる。解説文を書かれた東京理科大の吉岡教授に連絡を取り、解説文に基づく計算式では上左図と同じ結果が得られることを確認して頂いたので、プログラムの誤りの可能性は無くなった(と初めに書いたが実は非常に分かりづらいバグがあったことが後に判明、上図はそれを修正したもの)。上右図の計算がどのように行われたのか岡本さんに確認したところ、何と±105次まで計算しているとのこと。実際の光として現れる範囲さえ計算していれば大丈夫と思ったのは大きな間違いで、エバネッセント波となる成分もできるだけ多く計算しないといけないようだ。次数の２乗(階乗かも)に比例して計算時間がかかるので次数を増やすとやたら時間がかかるが、±10次ずつ増やして変化を見たのが下左図。

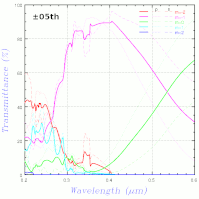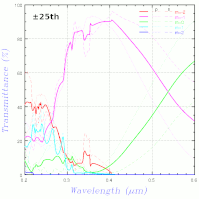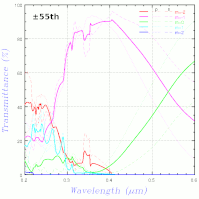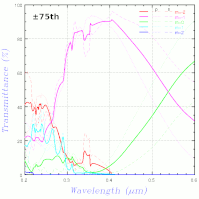
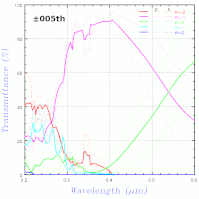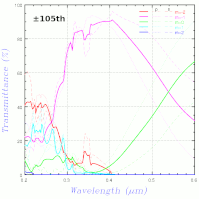
    ±30次程度でほとんど変化しなくなる。上右図は、岡本さんに±５次までの計算もお願いして変化を見たもの。次数が変わった際の変化が異なるが、岡本さんの話では、吉岡さんの方法は Enhanced T matrix 法でそれに対し岡本さんは S-matrix 法を用いているため手法が異なるということらしい。また、岡本さんは、屈折率は https://refractiveindex.info/) にある式を用い、groove 間隔 0.417μm (groove 密度 2398 l/mm) で計算しており、それに対しこちらの計算では屈折率はシグマ光機のデータを参照、groove 密度 2400 l/mm なので、ほんの少し条件が異なるが大体同じ答えになるようだ。

●GSolver V5.2 で計算してみる

    GSolver で通常の反射型回折格子を計算したことがあるが、透過型でも計算できるに違いないと思い、多分これだろうという設定をして計算してみた(GSolver のマニュアルには反射型の説明しか書いてないのでややこしいが、計算式としては反射も透過も区別する必要はないので当たり前か...)。SiO2 の屈折率データはソフト内データベースのものを参照。計算は±30次まで行った。

    計算結果の数値表は出て、指定した列の plot もできるのに、数値データを出力することができない...(以前から問題だったような気もする)。仕方がないので、s 偏光と p 偏光を別々に plot したものをキャプチャしたのが以下。その下が岡本さんの計算結果、一番下がこちらで計算したもの。

　　　　

　　　　

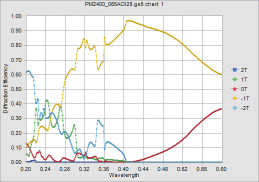
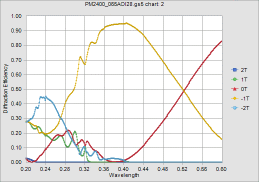
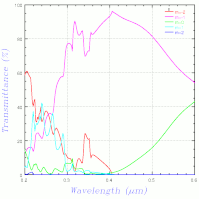
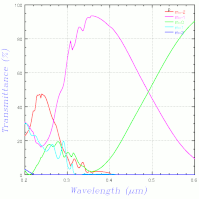
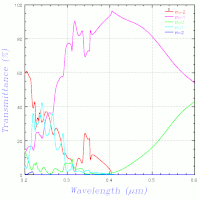
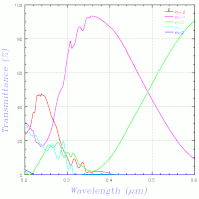
    こう見ると、GSolver の結果は少し違っているかも、という感じになってきた...

iwamuro@kusastro.kyoto-u.ac.jp